Optimization
Exploring optimization methods for solving structural and mechanical problems
This module dives into various optimization techniques, including gradient-based methods, genetic algorithms, and multi-objective optimization. These approaches are applied to structural and mechanical problems using MATLAB and ANSYS, providing insight into how optimization can enhance engineering designs.
Key assignments and simulations
Catenary Problem
Solved the classical catenary problem using optimization algorithms. Methods such as the Newton method, BFGS, DFP, and Conjugate Gradient were implemented and compared against analytical solutions to evaluate accuracy and performance.(Homework 1)
Potential Energy Optimization
Focused on minimizing potential energy for a hanging chain, leveraging optimization methods like SQP, Active Set, and Genetic Algorithms. MATLAB was used to compare different optimization algorithms in terms of convergence and computational efficiency.(Homework 2)
Application Case: Optimization of Cantilever Beam
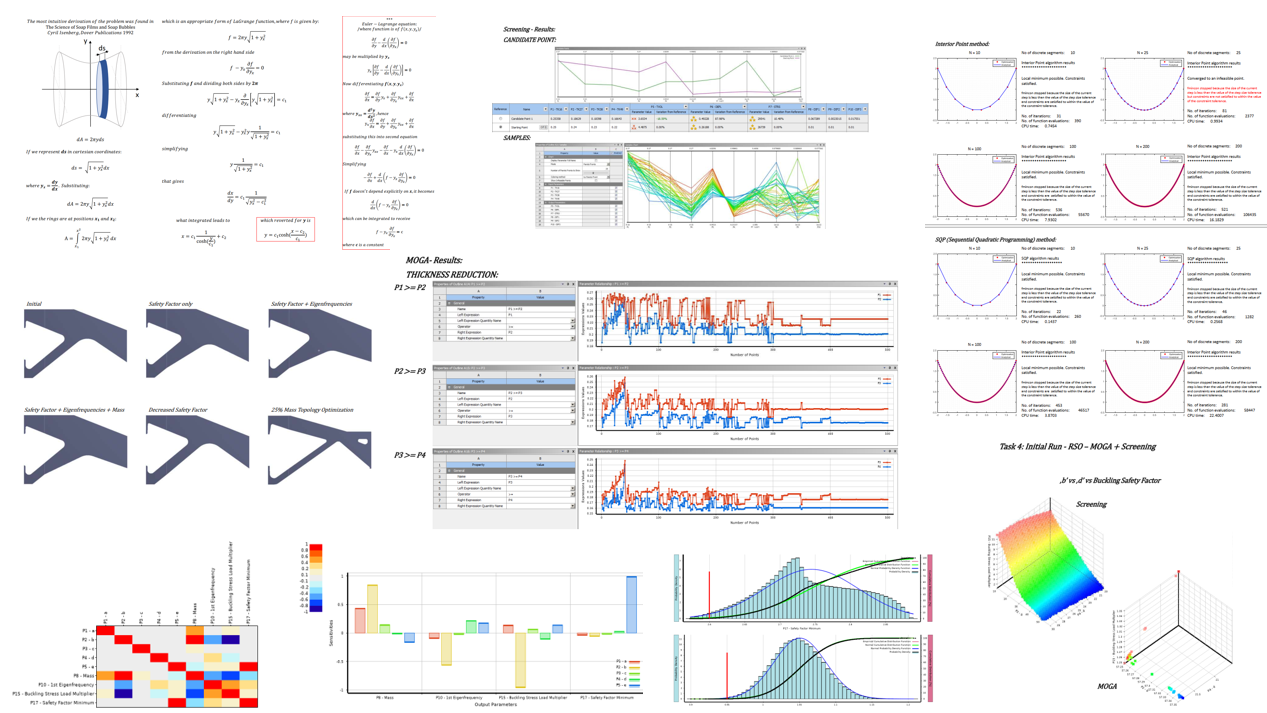
The application case explored multi-objective optimization for a cantilever beam. The problem involved minimizing both the beam’s deflection and equivalent stress, while optimizing its total volume. Using multi-objective genetic algorithms (MOGA), several design variants were analyzed. The study highlighted how sampling techniques and algorithm parameters affected the results.
Key conclusions:
Significant material savings (over 15%) were achieved while maintaining structural performance.
MOGA was efficient but required longer computation time compared to simpler screening methods.
Final Project: Structural Support Optimization
The final project involved a structural support system, focusing on reducing mass while maintaining safety and performance requirements. Initial topology optimization was conducted to explore different retained mass percentages (40%, 30%, and 20%), leading to validation and further refinement of the geometry.
Steps included:
Initial Design: A base block was analyzed for stress distribution under predefined loading conditions, revealing stress concentrations due to boundary conditions.
Topology Optimization: Various optimization runs were performed with different retained mass percentages. The 30% retained mass case was validated and refined for further improvements.
Parametric Optimization: The geometry was parametrized in ANSYS to further enhance the design, balancing structural integrity and manufacturing constraints.
Final Design: The final optimization achieved a 25% mass reduction with improved stress distribution, meeting all performance criteria.
This module provided hands-on experience with both gradient-based and evolutionary optimization methods, demonstrating their application to real-world engineering problems. The final project showcased how multi-objective optimization can significantly enhance structural designs by balancing multiple constraints.